Fórmulas Teoria dos Conjuntos

/ Fórmulas / Matemática /

Teoria dos Conjuntos

1. Símbolos

2. Utilizando: pertence, não pertence, está contido, não está contido, contém e não contém

Usamos $\in$ e $\not\in$ somente para relacionar elemento com conjunto.

Usamos $\subset$, $\not\subset$, $\supset$ e $\not\supset$ somente para relacionar um conjunto com outro conjunto.

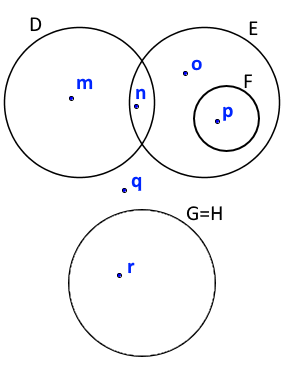
Relação entre conjuntos:

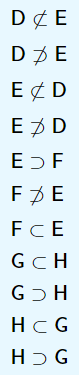
Relação entre elemento e conjunto:

3. Igualdade de conjuntos

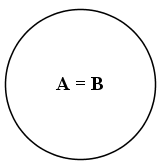
Dois conjuntos $A$ e $B$ são iguais se possuírem os mesmos elementos:

4. Conjunto vazio

É um conjunto que não possui elementos. É representado por $\left\{ \right\}$ ou $\varnothing$. O conjunto vazio está contido em todos os conjuntos.

5. Conjunto universo $ \left( \mathbb{U} \right)$

É o conjunto ao qual pertencem todos os elementos envolvidos em um determinado assunto ou estudo, e é simbolizado pela letra $\mathbb{U}$.

6. Diagramas de Venn

Diagramas de Venn são representações esquemáticas de conjuntos que contém todas as possíveis relações lógicas entre conjuntos.

Representação para 01 conjunto:

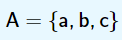
Representação para 02 conjuntos:

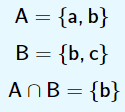
Representação para 03 conjuntos:

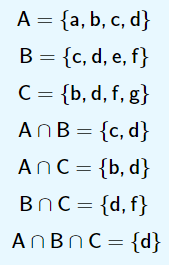
Representação para 04 conjuntos:

7. Interseção de conjuntos $\left(A \cap B \right)$

8. União de conjuntos $\left(A \cup B \right)$

Fórmula da União de dois conjuntos:

$n(A \cup B) = n(A) + n(B) - n(A \cap B)$

Fórmula da União de três conjuntos:

$n(A \cup B \cup C)= n(A) + n(B) + n(C) - n(A \cap B) - n(A \cap C) - n(B \cap C) + n(A \cap B \cap C)$

9. Diferença entre conjuntos $(A-B)$

10. Conjunto complementar $ \left( C^{B}_{A} \right) $

$C^{B}_{A}=A-B$

11. Conjunto complementar em relação ao universo$ \left( C^{A}_{U} \right) $

$C^{A}_{\mathbb{U}} = \mathbb{U} - A = \overline{A}$ ou $A' ($ não $A)$

12. Diferença simétrica entre dois conjuntos $ \left( \Delta \right) $

$A \Delta B = (A \cup B ) - (A \cap B)$

13. Conjuntos disjuntos

14. Conjunto das partes de um conjunto [P(A)]

É o conjunto de todos os subconjuntos desse conjunto.

$P(A) = 2^{n}$

$n$	:	número de elementos do conjunto A
$P(A)$	:	número de subconjuntos do conjunto A

Seja o conjunto $A = \left\{ a,b,c \right\}$, o conjunto das partes de $A$ é igual a:

$P(A) =$$ \left\{ \left\{ a \right\} , \left\{ b \right\} , \left\{ c \right\} , \left\{ a, b \right\} , \left\{ a, c \right\} , \left\{ b, c \right\} , \left\{ a, b, c \right\} , \varnothing \right\} $

Observação:

O conjunto vazio $ \left( \varnothing \right)$ é sempre subconjunto de qualquer conjunto.

15. Propriedades dos conjuntos

Simetria:

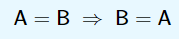
Idempotência:

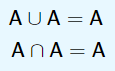
Absorção:

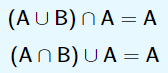
Comutatividade:

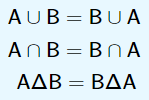
Associatividade:

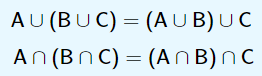
Distributividade:

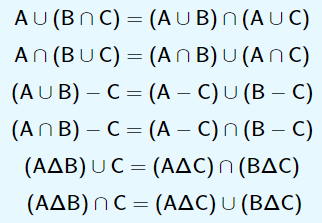
Transitividade:

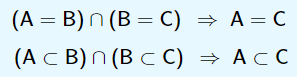
Leis de "De Morgan":

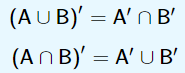
16. Produto cartesiano de dois conjuntos

$A x B = \left\{(x, y) \ | \ x \in A ∧ y \in B \right\} $

$($O produto cartesiano $A x B$ é o conjunto de pares ordenados $(x, y)$ tais que $x$ pertence a $A$ e $y$ pertence a $B)$

Sejam $A = \left\{a, b \right\}$ e $B = \left\{ c, d, e \right\}$

Então:

$A x B =$$ \left\{ (a ,c), (a, d), (a, e), (b, c), (b, d), (b, e) \right\}$

$B x A =$$ \left\{ (c, a), (c, b), (d, a), (d, b), (e, a), (e, b) \right\}$

Representação no diagrama de flechas

$A x B =$$ \left\{ (a, c), (a, d), (a, e), (b, c), (b, d), (b, e) \right\}$

17. Propriedades do produto cartesiano

Sejam $A, B$ e $C$ conjuntos, então:

$A x B \neq B x A$ (não comutatividade), quando $A \neq B, A \neq \varnothing$ e $B \neq \varnothing $

$A x (B x C) \neq (A x B) x C$ (não associatividade)

$A x (B \cup C) = (A x B) \cup (A x C)$ (distributividade em relação à união)

$A x (B \cap C) = (A x B) \cap (A x C)$ (distributividade em relação à interseção)

$(A x B) \cap (C x D) = (A \cap C) x (B \cap D) $

$A x B = \varnothing \Leftrightarrow (A = \varnothing ) ∨ (B = \varnothing ) $

$A x B =$$ B x A \Leftrightarrow (A = \varnothing ) ∨ (B = \varnothing ) ∨ (A = B)$