/ Matérias / Matemática /

Teoria dos Conjuntos

Problemas envolvendo 3 conjuntos: Exemplos e Exercícios

Ao todo são 92 pessoas entre Arquitetos (A), Urbanistas (U) e Engenheiros (E). Considere as informações a seguir, com as respectivas legendas, e sabendo que uma pessoa pode exercer mais de uma dessas funções.

I. São A e U apenas, 15 pessoas.
II. São A e E apenas, 12 pessoas.
III. São E e U apenas, 7 pessoas.
IV. Dentre aqueles que exercem apenas uma dessas funções, há quatro Urbanistas a mais que Arquitetos, e quatro Engenheiros a mais que Urbanistas.
V. Os que exercem apenas uma função, ao todo, são quatro pessoas a menos do que aqueles que exercem as três funções.

A partir dessas informações, qual é o número total de engenheiros?

Vamos desenhar o Diagrama de Venn:

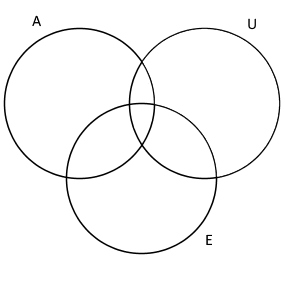
Vamos representar cada parte do Diagrama de Venn por uma letra. Vamos usar as seguintes letras: F, G, H, I, J, K, L.

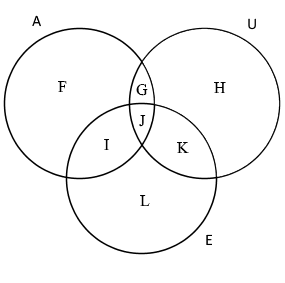
Como temos ao todo 92 pessoas entre estas 3 profissões, então:

$F + G + H + I + J + K + L = 92$

Da informação que são A e U apenas, 15 pessoas, temos que:

$G = 15$

Da informação que são A e E apenas, 12 pessoas, temos que:

$I = 12$

Da informação que são E e U apenas, 7 pessoas, temos que:

$K = 7$

Vamos analisar a próxima informação: Dentre aqueles que exercem apenas uma dessas funções, há quatro Urbanistas a mais que Arquitetos, e quatro Engenheiros a mais que Urbanistas.

A parte em azul diz que as informações só valem para as pessoas localizadas em F, H, L.

Tendo em vista o dito na parte azul, a parte em vermelho diz que:

$H = F + 4$

Tendo em vista o dito na parte azul, a parte em verde diz que:

$L = H + 4$

Agora, vamos ver a última informação que o enunciado nos dá: Os que exercem apenas uma função, ao todo, são quatro pessoas a menos do que aqueles que exercem as três funções.

A parte em azul é F + H + L e a parte em vermelho é J. Então:

$F + H + L = J - 4$

Então, o enunciado nos deu as seguintes informações:

$\style{color:red}{F+G+H+I+J+K+L = 92}$

$G=15$

$I=12$

$K=7$

$\style{color:blue}{H=F+4}$

$\style{color:#56EC3C}{L=H+4}$

$\style{color:#E73CEC}{F + H + L = J - 4}$

Vamos trocar os valores de G, I, K na equação em vermelho:

$F+15+H+12+J+7+L = 92$

$F+H+J+L = 92 - 15 -12 -7$

$\style{color:darkorange}{F+H+J+L = 58}$

Vamos colocar os valores de F, J e L em função do valor de H. Veja a equação em azul:

$H=F+4$

$\colorbox{yellow}{$F=H-4$}$

Agora, veja a equação em verde. O valor de L já está em função de H:

$\colorbox{yellow}{$L=H+4$}$

Vamos trocar os valores de F e L na equação em rosa.

$(H-4) + H + (H+4) = J - 4$

$3H = J - 4$

$\colorbox{yellow}{$J = 3H + 4$}$

Vamos trocar os valores dentro das caixas amarelas na equação em laranja.

$\style{color:darkorange}{F+H+J+L = 58}$

$(H-4) + H + (3H+4) + (H+4) = 58$

$6H + 4 = 58$

$H = 9$

Como H = 9, então:

$J = 31$

$L = 13$

$F = 5$