/ Matérias / Matemática /

Teoria dos Conjuntos

Problemas envolvendo 3 conjuntos: Exemplos e Exercícios

Problema 1 - Uma pesquisa com 1000 pessoas concluiu que: 450 pessoas gostam de ver a Globo. 430 pessoas gostam da SBT. 340 gostam da Band. 200 gostam da Globo e SBT. 180 gostam da Globo e Band. 100 gostam da Band e SBT. 30 gostam dos três canais. Então:

a) Qual é o número de pessoas que não gosta de nenhum desses canais?
b) Qual é o número de pessoas que gosta de apenas de um desses canais?

Primeiro vamos desenhar os três conjuntos. Como uma das perguntas são quantas pessoas gostam de nenhum dos canais, vamos desenhar também o conjunto universo:

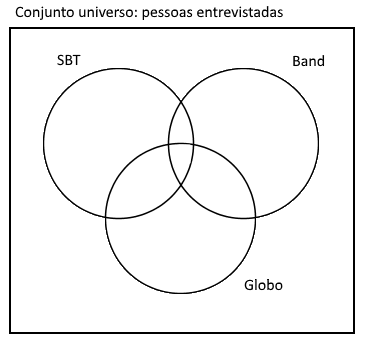
Agora vamos começar a colocar as informações no desenho. É comum ser mais fácil começar pela informação da interseção dos três conjuntos, que nesse caso são as pessoas que gostam ao mesmo tempo de Globo, SBT e Band:

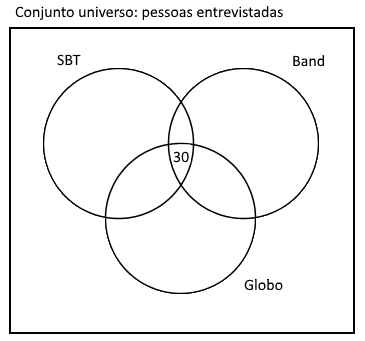
200 pessoas gostam da Globo e SBT, então 170 (200 menos 30) pessoas gostam da SBT e Globo mas não gostam da Band:

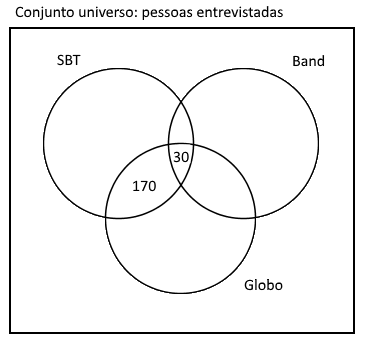
180 pessoas gostam da Globo e Band, então 150 (180 menos 30) pessoas gostam da Globo e Band mas não gostam da SBT:

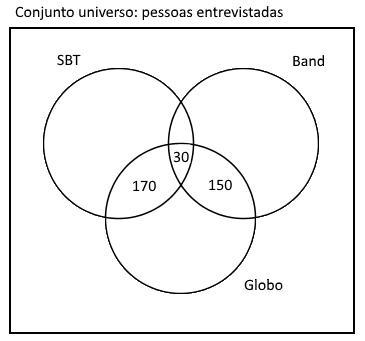
100 pessoas gostam da Band e SBT, então 70 (100 menos 30) pessoas gostam da Band e SBT mas não gostam da Globo:

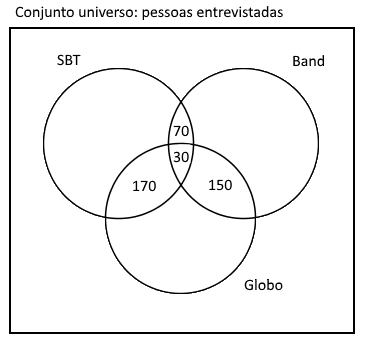
450 pessoas gostam da Globo, então:

$450-170-30-150 = 100$

100 pessoas gostam só da Globo.

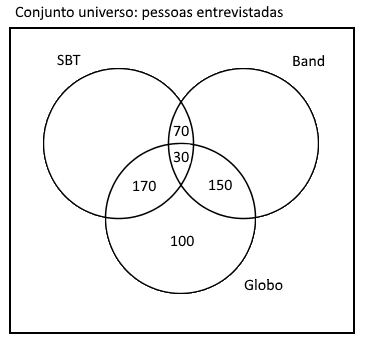
430 pessoas gostam da SBT, então:

$430-170-30-70 = 160$

160 pessoas gostam só da SBT.

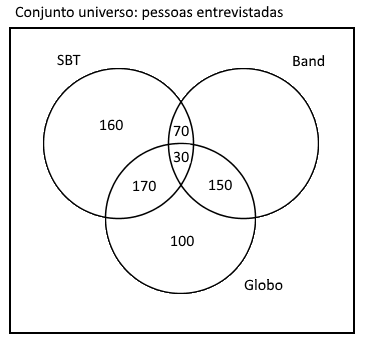
340 pessoas gostam da Band, então:

$340-70-30-150 = 90$

90 pessoas gostam só da Band.

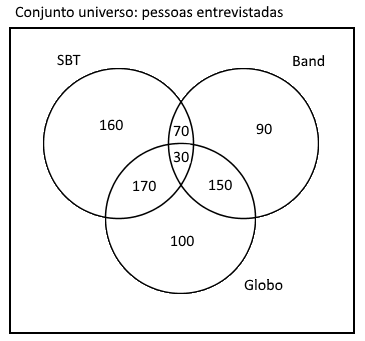
Como 1000 pessoas foram entrevistadas, o total de pessoas que não gostam de nenhum dos 3 canais é:

$1000 - 160 - 70 - 90 - 170 - 30 -150 - 100 = 230$

230 pessoas não gostam de nenhum dos 3 canais:

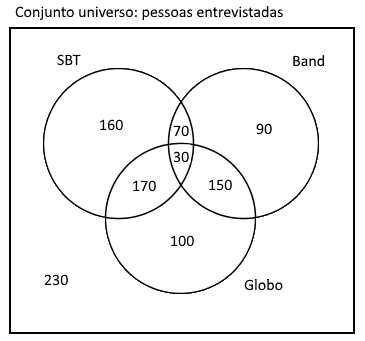
A primeira pergunta é: "a) Qual é o número de pessoas que não gosta de nenhum desses canais?". A resposta é 230.

A segunda pergunta é: "b) Qual é o número de pessoas que gosta de apenas de um desses canais?". Esta pergunta quer saber a soma das pessoas que gostam só de SBT, que gostam só de Band e que gostam só de Globo:

$160 + 90 + 100 = 350$

a) 230 pessoas
b) 350 pessoas