ent6 Teoria dos Conjuntos: Problemas envolvendo 2 conjuntos: Exemplos e Exercícios 
/ Matérias / Matemática /

Teoria dos Conjuntos

16

Problemas envolvendo 2 conjuntos: Exemplos e Exercícios

Problema 1 - Numa academia de ginástica, 120 frequentadores praticam natação ou musculação. Sabe-se que 72 praticam natação e 56 praticam musculação. Desse modo, o total de frequentadores que praticam somente musculação é:
Temos dois conjuntos, os das pessoas que praticam natação e os dos que praticam musculação. Vamos desenhar o Diagrama de Venn para 2 conjuntos:
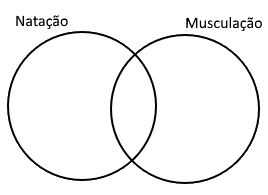
Veja a seguinte informação que o enunciado nos dá: 72 praticam natação. Estes 72 estão distribuídos entre os que só praticam natação e os que praticam natação e musculação, conforme área pintada no desenho abaixo. Então, não conseguimos ainda colocar este número no desenho.
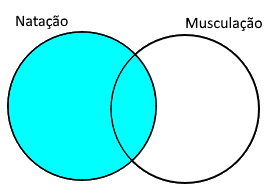
A próxima informação no enunciado é: 56 praticam musculação. Ele representa a parte pintada abaixo. Também não conseguimos colocar essa informação no Diagrama de Venn:
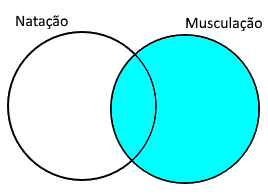
Não estamos conseguindo colocar as informações na nossa imagem. Para resolver isso, vamos dizer que a interseção entre os conjuntos tem um número "x" de pessoas:
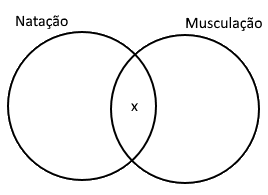
Agora podemos voltar para a primeira informação: 72 praticam natação. Como x pessoas praticam natação e musculação, então aqueles que só praticam natação será 72 - x:
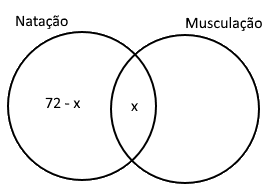
Utilizando o mesmo pensamento, os que praticam só musculação será 56 - x:
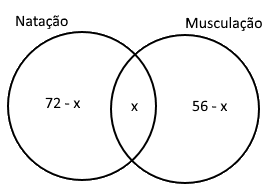
Se somarmos cada um desses valores devemos necessariamente chegar no total de pessoas que vão para a academia:
$(72 - x) + (x) + (56-x) = 120$

$72-x+x+56-x = 120$

$128 - x = 120$

$- x = 120 - 128$

$- x = -8$

$x = 8$
Os que praticam somente musculação são 56 - x. Como x é igual a 8, então, são 48 pessoas que praticam somente musculação.
48 pessoas praticam somente musculação.




16 de 20







desenvolvido por


Copyright © 2023 Central Exatas
Todos os direitos reservados.