/ Matérias / Matemática /

Sistemas Lineares

Regra de Cramer: Exemplos e Exercícios

Exemplo 2 - Calcule o valor de $x$, $y$ e $z$ do sistema de equações abaixo:

$\begin{cases} x+y+z=1 \\ 2x-y-3z=2 \\ 2x+y-z=1 \\ \end{cases}$

Pela regra de Cramer matricialmente temos $A.B = C$:

$\begin{bmatrix} 1 & 1 & 1 \\ 2 & -1 & -3 \\ 2 & 1 & -1 \\ \end{bmatrix} . \begin{bmatrix} x \\ y \\ z \\ \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 1 \\ \end{bmatrix}$

$x=\dfrac{det(A_{x})}{det(A)}$

$y=\dfrac{det(A_{y})}{det(A)}$

$z=\dfrac{det(A_{z})}{det(A)}$

Vamos calcular o determinante da matriz incompleta utilizando a regra de Sarrus:

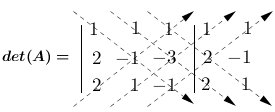
$det(A) = 1.(-1).(-1) + 1.(-3).2 + 1.2.1 \hspace{0.2em} - 2.(-1).1 \hspace{0.2em} - 1.(-3).1 \hspace{0.2em} - (-1).2.1$

$det(A) = 1 - 6 + 2 + 2 + 3 + 2$

$det(A) = 4$

A matriz $A_{x}$ é obtida com a substituição da 1ª coluna da matriz $A$, que contém os coeficientes de $x$, pela coluna da matriz $C$, que são os termos independentes das equações, portanto:

$A_{x} = \begin{bmatrix} 1 & 1 & 1 \\ 2 & -1 & -3 \\ 1 & 1 & -1 \\ \end{bmatrix}$

A matriz $A_{y}$ é obtida com a substituição da 2ª coluna da matriz $A$, que contém os coeficientes de $y$, pela coluna da matriz $C$, que são os termos independentes das equações, portanto:

$A_{y} = \begin{bmatrix} 1 & 1 & 1 \\ 2 & 2 & -3 \\ 2 & 1 & -1 \\ \end{bmatrix}$

A matriz $A_{z}$ é obtida com a substituição da 3ª coluna da matriz $A$, que contém os coeficientes de $z$, pela coluna da matriz $C$, que são os termos independentes das equações, portanto:

$A_{z} = \begin{bmatrix} 1 & 1 & 1 \\ 2 & -1 & 2 \\ 2 & 1 & 1 \\ \end{bmatrix}$

Vamos calcular os determinantes $det(A_{x})$, $det(A_{y})$ e $det(A_{z})$.

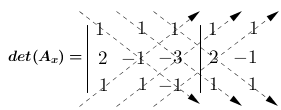
$det(A_{x}) = 1.(-1).(-1) + 1.(-3).(1) + 1.2.(1) \hspace{0.2em} - 1.(-1).1 \hspace{0.2em} - 1.(-3).1 \hspace{0.2em} - (-1).2.1$

$det(A_{x}) = 1 - 3 + 2 + 1 + 3 + 2$

$det(A_{x}) = 6$

$det(A_{y}) = 1.2.(-1) + 1.(-3).(2) + 1.2.1 - 2.2.1 - 1.(-3).1 - (-1).2.1$

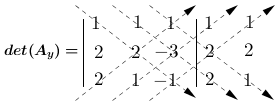
$det(A_{y}) = - 2 - 6 + 2 - 4 + 3 + 2$

$det(A_{y}) = - 5$

$det(A_{z}) = 1.(-1).1 + 1.2.2 + 1.2.1 - 2.(-1).1 - 1.2.1 - 1.2.1$

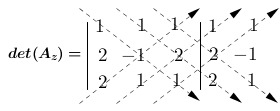
$det(A_{z}) = - 1 + 4 + 2 + 2 - 2 - 2$

$det(A_{z}) = 3$

Finalmente vamos calcular o valor de $x$, $y$ e $z$:

$x=\dfrac{det(A_{x})}{det(A)}=\dfrac{6}{4}$

$x=1,5$

$y=\dfrac{det(A_{y})}{det(A)}=\dfrac{-5}{4}$

$y=-1,25$

$z=\dfrac{det(A_{z})}{det(A)}=\dfrac{3}{4}$

$z=0,75$

$x = 1,5$

$y = -1,25$

$z = 0,75$

7 de 9

Definição de sistema linear

Métodos de resolução de sistemas lineares

Métodos de resolução de sistemas lineares: Exemplos e Exercícios

Regra de Cramer

Regra de Cramer: Exemplos e Exercícios

Classificação e análise de um sistema linear

Sistemas homogêneos