Fechar 
-
-
- FÓRMULAS - GERAL
- FÓRMULAS DE CONJUNTOS
- FÓRMULAS DE ÁLGEBRA
- FÓRMULAS DE TRIGONOMETRIA
- FÓRMULAS DE EQUAÇÕES
- FÓRMULAS DE INEQUAÇÕES
- FÓRMULAS DE FUNÇÕES
- FÓRMULAS DE MATRIZES, DETERMINANTES E SISTEMAS LINEARES
- FÓRMULAS DE GEOMETRIA: 2D
- FÓRMULAS DE GEOMETRIA: 3D
- FÓRMULAS DE GEOMETRIA ANALÍTICA
- FÓRMULAS - OUTROS
-
-
xxxx
-
xxxx
Retângulo
Retângulo: Exemplos e Exercícios
Quanto mede o comprimento da circunferência ($C = 2 . \pi . r$), circunscrita num retângulo com lados medindo 15 cm e 10 cm?
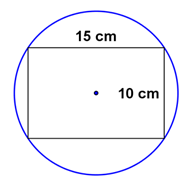
Vamos calcular o raio da circunferência circunscrita:
$r = \dfrac{\sqrt[]{a^2 + b^2}}{2}$
$r = \dfrac{\sqrt[]{15^2 + 10^2}}{2}$
$r = \dfrac{\sqrt[]{225 + 100}}{2}$
$r = \dfrac{\sqrt[]{325}}{2}$
$r = 18, \hspace{-0.1em} 03 \ cm$
$r = \dfrac{\sqrt[]{15^2 + 10^2}}{2}$
$r = \dfrac{\sqrt[]{225 + 100}}{2}$
$r = \dfrac{\sqrt[]{325}}{2}$
$r = 18, \hspace{-0.1em} 03 \ cm$
Agora vamos calcular o comprimento da circunferência:
$C = 2. \pi . r$
$C = 2 . 3, \hspace{-0.1em} 14 . 18, \hspace{-0.1em} 03$
$C = 113, \hspace{-0.1em} 23 \ cm$
$C = 2 . 3, \hspace{-0.1em} 14 . 18, \hspace{-0.1em} 03$
$C = 113, \hspace{-0.1em} 23 \ cm$
O comprimento da circunferência é de 113,23 cm.
6 de 6
