Fechar 
-
-
- FÓRMULAS - GERAL
- FÓRMULAS DE CONJUNTOS
- FÓRMULAS DE ÁLGEBRA
- FÓRMULAS DE TRIGONOMETRIA
- FÓRMULAS DE EQUAÇÕES
- FÓRMULAS DE INEQUAÇÕES
- FÓRMULAS DE FUNÇÕES
- FÓRMULAS DE MATRIZES, DETERMINANTES E SISTEMAS LINEARES
- FÓRMULAS DE GEOMETRIA: 2D
- FÓRMULAS DE GEOMETRIA: 3D
- FÓRMULAS DE GEOMETRIA ANALÍTICA
- FÓRMULAS - OUTROS
-
-
xxxx
-
xxxx
Raciocínio Lógico
Operadores Lógicos: Operador "e"
Para entender o operador "e", vamos usar um exemplo. Veja abaixo:
Vou à praia e ao shopping
O que precisa acontecer para essa proposição toda ser verdadeira? Eu devo ir à praia e também ir ao shopping. Se eu não for a estes lugares ou se for a apenas um deles, eu não terei dito a verdade, não é?
Para entender melhor, tente pensar em todas as combinações que podemos fazer em relação à veracidade dessa proposição. Só existem 4 combinações possíveis, que são:
| Fui à praia | e | fui ao shopping |
| Fui à praia | e | não fui ao shopping |
| Não fui à praia | e | fui ao shopping |
| Não fui à praia | e | não fui ao shopping |
Podemos colocar essas combinações em uma tabela para facilitar a visualização:
Na 1ª linha, eu fui aos dois lugares. Logo, cumpri o que disse.
Na 2ª linha, fui à praia, mas não fui ao shopping. Assim, não cumpri o que disse.
Na 3ª linha, não fui à praia, mas fui ao shopping. Portanto, não cumpri o que disse.
Na 4ª linha, não fui à praia e não fui ao shopping. Não cumpri o que disse.
Na 2ª linha, fui à praia, mas não fui ao shopping. Assim, não cumpri o que disse.
Na 3ª linha, não fui à praia, mas fui ao shopping. Portanto, não cumpri o que disse.
Na 4ª linha, não fui à praia e não fui ao shopping. Não cumpri o que disse.
Símbolo do operador "e":
Veja a proposição abaixo:
Vou à praia e ao shopping
| $p$ | : | vou à praia |
| $q$ | : | (vou) ao shopping |
| $\wedge$ | : | "e" |
Assim, podemos reescrever a proposição da seguinte forma:
$p \wedge q$
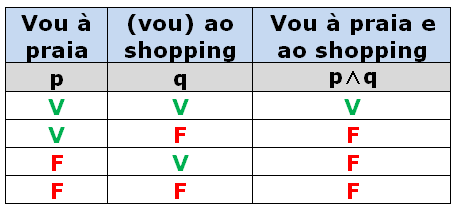
Tabela-verdade do operador "e":
A tabela acima é conhecida como tabela-verdade e ela é escrita formalmente desta maneira:
5 de 33
1
Fundamentos do Raciocínio Lógico
2
Fundamentos do Raciocínio Lógico: Símbolos
3
Fundamentos do Raciocínio Lógico: Princípios
4
Operadores Lógicos
5
Operadores Lógicos: Operador "e"
6
Operadores Lógicos: Operador "ou"
7
Operadores Lógicos: Operador "ou... ou..." (ou exclusivo)
8
Operadores Lógicos: Operador "se... então..."
9
Operadores Lógicos: Operador "se e somente se"
10
Resumo dos operadores lógicos
11
Operador Não (negação)
12
Proposições simples e compostas
13
Como montar uma tabela-verdade: Para 2 proposições simples
14
Como montar uma tabela-verdade: Para 3 proposições simples
15
Número de linhas da tabela-verdade
16
Usando a tabela-verdade para resolver problemas
17
Ordem de resolução de proposições sem parênteses
18
O significado dos operadores no Raciocínio Lógico não é o mesmo do significado deles no Português
19
O Raciocínio Lógico não necessariamente se importa com o mundo real
20
Não se confunda com os símbolos
21
Tautologia
22
Contradição
23
Contingência
24
Tautologia, Contradição e Contingência: Resumo
25
Equivalência entre proposições
26
Negação de proposições
27
Lógica de Argumentação: Definição
28
Argumento Válido
29
Argumento Inválido
30
Formas de verificação da validade de um argumento
31
Formas de verificação da validade de um argumento: Utilizando diagramas de conjuntos
32
Formas de verificação da validade de um argumento: Considerando as premissas verdadeiras
33
Formas de verificação da validade de um argumento: Considerando a conclusão falsa
