/ Matérias / Matemática /

Raciocínio Lógico

Formas de verificação da validade de um argumento: Utilizando diagramas de conjuntos

Recomenda-se o uso de diagramas de conjuntos, para verificação de um argumento, quando as premissas estiverem na forma de proposições categóricas.

As proposições categóricas apresentam palavras como todo, algum e nenhum ou sinônimos.

Exemplo:

Se é verdade que "algum X é Y" e que "nenhum Z é Y", então é necessariamente verdadeiro que:
(A) algum X não é Z.
(B) algum X é Z.
(C) nenhum X é Z.
(D) algum Z é X.
(E) nenhum Z é X.

Vamos fazer o diagrama de Venn para 2 conjuntos:

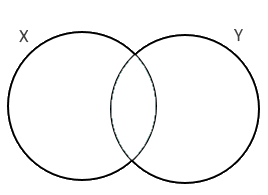
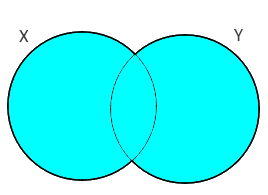
Vamos começar pela afirmação que "alguma X é Y". Essa afirmação faz com que a parte compartilhada entre os conjuntos X e Y nunca esteja vazia. Desta forma, teremos 4 possibilidades:

1) Todas as partes dos conjuntos tem elementos:

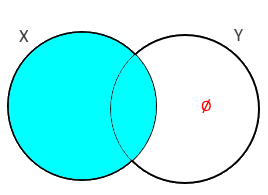
2) A parte só para o conjunto X tem elemento e a parte só para Y não:

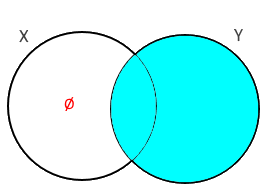
3) A parte só para o conjunto X não tem elemento e parte só para Y tem:

4) A parte só para o conjunto X e para só o Y estão ambas vazias:

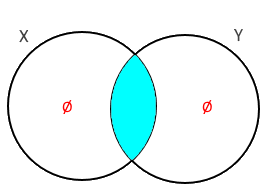
Agora vamos ver a afirmação "nenhum Z é Y". Se formos fazer o desenho de todas as possibilidades vamos ter desenhos demais para fazer. Porém, observe que se nenhum Z é Y, então o Z não vai estar na parte do meio entre X e Y. Aquela parte, que conforme vimos, nunca está vazia. Desta forma, sempre haverá algum X que não é Z.

Letra A.