Raciocínio Lógico



Usando a tabela-verdade para resolver problemas
Agora vamos mostrar como a tabela-verdade é uma ótima ferramenta para resolver problemas.
Imagine que queremos saber em quais casos a proposição $(p \wedge q)\rightarrow(p \vee q)$ será V ou F . Tentar fazer de cabeça é bem complicado. O melhor é usar a tabela-verdade.
Para montar as colunas da tabela-verdade seguimos 3 passos:
1) Nas primeiras colunas colocamos todas as proposições simples que compõem a proposição inteira. Nesse caso são "$p$" e "$q$".
2) Depois colocamos as proposições compostas que compõem a proposição composta toda. Nesse caso são "$p \wedge q$" e "$p \vee q$".
3) Na última coluna colocamos a proposição composta inteira.
A tabela-verdade ficará assim:

Os valores de "$p$" e "$q$" são todas as combinações possíveis de V e F , conforme mostrado no slide sobre montar tabela-verdade:

Para completar a terceira e quarta colunas vamos usar as lógicas dos operadores "e" e "ou":
$p \wedge q$ só será verdadeiro quando ambos foremV ao mesmo tempo.
$p \vee q$ será verdadeiro se pelo menos um forV.
$p \wedge q$ só será verdadeiro quando ambos forem
$p \vee q$ será verdadeiro se pelo menos um for

Nós já sabemos como dar valores de V ou F para a proposição $p \rightarrow q$. Mas o que iremos fazer com a proposição $(p \wedge q) \rightarrow (p \vee q)$??
O procedimento vai ser igual ao que fazemos para $p \rightarrow q$, mas nesse caso "$p$" será $(p \wedge q)$ e "$q$" será $(p \vee q)$. Veja a comparação:
$(p \wedge q) \rightarrow (p \vee q)$
$p \rightarrow q$
$p \rightarrow q$
Sabemos que $p \rightarrow q$ só é falso quando p = V e q = F . Observando a tabela-verdade, não há nenhum caso em que simultaneamente $(p \wedge q)$ é V e $(p \vee q)$ é F . Logo a proposição inteira vai ser sempre V !
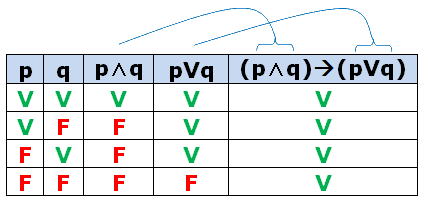
Não seria tão fácil chegar nessa conclusão sem usar a tabela-verdade.
1
Fundamentos do Raciocínio Lógico
2
Fundamentos do Raciocínio Lógico: Símbolos
3
Fundamentos do Raciocínio Lógico: Princípios
4
Operadores Lógicos
5
Operadores Lógicos: Operador "e"
6
Operadores Lógicos: Operador "ou"
7
Operadores Lógicos: Operador "ou... ou..." (ou exclusivo)
8
Operadores Lógicos: Operador "se... então..."
9
Operadores Lógicos: Operador "se e somente se"
10
Resumo dos operadores lógicos
11
Operador Não (negação)
12
Proposições simples e compostas
13
Como montar uma tabela-verdade: Para 2 proposições simples
14
Como montar uma tabela-verdade: Para 3 proposições simples
15
Número de linhas da tabela-verdade
16
Usando a tabela-verdade para resolver problemas
17
Ordem de resolução de proposições sem parênteses
18
O significado dos operadores no Raciocínio Lógico não é o mesmo do significado deles no Português
19
O Raciocínio Lógico não necessariamente se importa com o mundo real
20
Não se confunda com os símbolos
21
Tautologia
22
Contradição
23
Contingência
24
Tautologia, Contradição e Contingência: Resumo
25
Equivalência entre proposições
26
Negação de proposições
27
Lógica de Argumentação: Definição
28
Argumento Válido
29
Argumento Inválido
30
Formas de verificação da validade de um argumento
31
Formas de verificação da validade de um argumento: Utilizando diagramas de conjuntos
32
Formas de verificação da validade de um argumento: Considerando as premissas verdadeiras
33
Formas de verificação da validade de um argumento: Considerando a conclusão falsa





