/ Matérias / Matemática /

Polinômio

Divisão de polinômios: Exemplos e Exercícios

Vamos dividir o polinômio $P(x)=12x^{3}-4x+9$ por $D(x) = 2x^{2}+x+3$

Vamos completar o polinômio $P(x)$ acrescentando o termo faltante que é o $0x^{2}$.

Agora vamos utilizar o modelo acima para realizar a divisão.

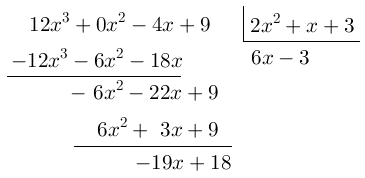
Descrição da resolução:

1º Divide-se a parcela $12x^{3}$ do dividendo pela primeira parcela $2x^{2}$ do divisor obtendo-se $6x$.

2º Multiplicamos o $6x$ do quociente pelo $2x^{2}$ do divisor e colocamos o resultado com o sinal trocado $\left( -12x^{3} \right)$ abaixo de $12x^{3}$ do dividendo.

3º Repetimos a mesma operação multiplicando $6x$ do quociente por $x$ e por $3$ do divisor e trocando o sinal obtemos $-6x^{2}$ e $-18x$ que são colocados abaixo de $0x^{2}$ e $-4x$ do dividendo.

4º Realizamos a operação de soma/subtração obtendo $-6x^{2} -22x$ e em seguida abaixamos o número $9$ do dividendo.

5º Dividimos a parcela $-6x^{2}$ por $2x^{2}$ do dividendo obtendo o número $-3$.

6º Multiplicamos o $-3$ do quociente pelo $2x^{2}$ do divisor e colocamos o resultado com o sinal trocado $\left( 6x^{2} \right)$, abaixo de $-6x^{2}$.

7º Repetimos a mesma operação multiplicando $-3$ do quociente por $x$ e por $3$ do divisor e trocando o sinal obtemos $3x$ e $9$ que são colocados abaixo de $-22x$ e do $9$.

8º Realizamos a operação de soma/subtração obtendo $-19x + 18$ que é o resto da divisão.

Resultado da divisão de P(x) por D(x):

$Q(x) = 6x - 3$

$R(x) = -19x + 18$