Fechar 
-
-
- FÓRMULAS - GERAL
- FÓRMULAS DE CONJUNTOS
- FÓRMULAS DE ÁLGEBRA
- FÓRMULAS DE TRIGONOMETRIA
- FÓRMULAS DE EQUAÇÕES
- FÓRMULAS DE INEQUAÇÕES
- FÓRMULAS DE FUNÇÕES
- FÓRMULAS DE MATRIZES, DETERMINANTES E SISTEMAS LINEARES
- FÓRMULAS DE GEOMETRIA: 2D
- FÓRMULAS DE GEOMETRIA: 3D
- FÓRMULAS DE GEOMETRIA ANALÍTICA
- FÓRMULAS - OUTROS
-
-
xxxx
-
xxxx
Polígonos
Ângulos externos de um polígono convexo
São os ângulos que estão no exterior do polígono, formado entre um de seus lados e o prolongamento do lado consecutivo a ele.
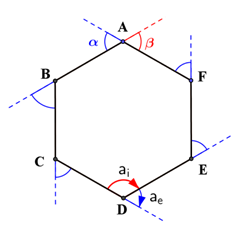
Considerando o segmento $\overline{AB}$ e prolongando o segmento $\overline{FA}$ obtemos o ângulo externo $\alpha$ .
A outra opção seria considerar o segmento $\overline{AF}$ e prolongar o segmento $\overline{BA}$ obtendo assim o ângulo $\beta$ , que é igual ao ângulo $\alpha$ pois são ângulos opostos pelo vértice.
A soma dos ângulos externos de um polígono convexo é sempre igual a 360°.
Um ângulo interno $(a_i)$ e um ângulo externo $(a_e)$ adjacente a ele são suplementares (somam 180°).
No caso de um polígono regular, cujos ângulos externos são iguais, podemos obter a medida de um ângulo com a seguinte fórmula:
$a_e = \dfrac{360}{n}$
| $a_{e}$ | : | ângulo externo |
| n | : | número de lados do polígono regular |
9 de 12
1
Definição de Polígonos
2
Tipos de Polígonos
3
Classificação dos polígonos
4
Diagonal de um polígono
5
Diagonal de um polígono: Exemplos e Exercícios
6
Diagonal de um polígono: Exemplos e Exercícios
7
Ângulos internos de um polígono convexo
8
Ângulos internos de um polígono convexo: Exemplos e Exercícios
9
Ângulos externos de um polígono convexo
10
Ângulos externos de um polígono convexo: Exemplos e Exercícios
11
Ângulos externos de um polígono convexo: Exemplos e Exercícios
12
Quadriláteros notáveis - Diagrama dos quadriláteros
