/ Matérias / Matemática /

Pipa

Pipa: Exemplos e Exercícios

Na figura abaixo calcule a área e o perímetro da pipa (as unidades estão em cm).

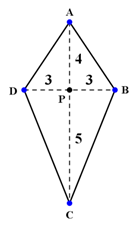
Vamos analisar os dados da figura:

$d_1 = 3 +3 = 6cm \qquad$ (diagonal menor)

$d_2 = 4 + 5 = 9cm \qquad$ (diagonal maior)

Com estes dados podemos calcular a área da pipa:

$A = \dfrac{d_1 . d_2}{2}$

$A = \dfrac{6.9}{2}$

$\colorbox{lightgreen}{$A = 27 \ cm^2$}$

Para o cálculo do perímetro temos a seguinte fórmula:

$P = 2(a+b)$

Precisamos encontrar as medidas dos lados a e b da pipa:

Considerando o triângulo retângulo APB podemos calcular o lado a da pipa com a utilização do teorema de Pitágoras:

$a^2 = 4^2 + 3^2$

$a^2 = 16+9$

$a = \sqrt[]{25}$

$a = 5 \ cm$

Agora considerando o triângulo retângulo PCB podemos calcular o lado b da pipa com a utilização também do teorema de Pitágoras:

$b^2 = 5^2 + 3^2$

$b^2 = 25+9$

$b = \sqrt[]{34}$

$b = 5, \hspace{-0.1em} 83 \ cm$

Agora podemos calcular o perímetro da pipa:

$P = 2(a+b)$

$P = 2(5 + 5, \hspace{-0.1em} 83)$

$P = 2(10, \hspace{-0.1em} 83)$

$\colorbox{lightgreen}{$P = 21, \hspace{-0.1em} 66 \ cm$}$

A área da pipa é 27 cm² e o perímetro é de 21,66 cm.

4 de 4