/ Matérias / Matemática /

Matrizes e Determinantes

Cálculo da matriz inversa com a utilização da matriz adjunta

Método aplicável para matrizes quadradas de 2ª ordem ou superior.

$A^{-1}=\dfrac{\overline{A}}{det(A)}$

$\overline{A}$ - matriz adjunta (transposta da matriz de cofatores).

Calcular a inversa da matriz A abaixo:

$A= \begin{bmatrix} 3 & 2 & 5 \\ 2 & 6 & 8 \\ 5 & 7 & 4 \\ \end{bmatrix}$

Para calcular a matriz adjunta $\overline{A}$ devemos primeiro obter a matriz de cofatores:

Calculando os cofatores dos elementos da matriz $A$, encontramos:

$A_{11} = -32$

$A_{12} = 32$

$A_{13} = -16$

$A_{21} = 27$

$A_{22} = -13$

$A_{23} = -11$

$A_{31} = -14$

$A_{32} = -14$

$A_{33} = 14$

Portanto a matriz de cofatores associada à matriz A é:

$Cof(A) = \begin{bmatrix} -32 & 32 & -16 \\ 27 & -13 & -11 \\ -14 & -14 & 14 \\ \end{bmatrix}$

A matriz adjunta $\overline{A}$ é a transposta da matriz de cofatores, portanto:

$\overline{A} = \begin{bmatrix} -32 & 27 & -14 \\ 32 & -13 & -14 \\ -16 & -11 & 14 \\ \end{bmatrix}$

Agora calculando o $det(A)$ pela regra de Sarrus encontramos.

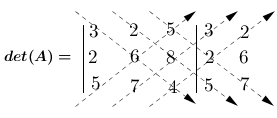
$det(A) = 3.6.4 + 2.8.5 + 5.2.7 \hspace{0.2em} - 5.6.5 \hspace{0.2em} - 7.8.3 \hspace{0.2em} - 4.2.2$

$det(A) = 72 + 80 + 70 \hspace{0.2em} - 150 \hspace{0.2em} - 168 - 16$

$det(A) = -112$

Finalmente vamos substituir os valores encontrados na fórmula para encontrar a matriz inversa de A:

$A^{-1}=\dfrac{\overline{A}}{det(A)}$

$A^{-1}=\dfrac{ \begin{bmatrix} -32 & 27 & -14 \\ 32 & -13 & -14 \\ -16 & -11 & 14 \\ \end{bmatrix} }{-112}$

$A^{-1} = \begin{bmatrix} 0,2857 & -0,241 & 0,125 \\ -0,2857 & 0,116 & 0,125 \\ 0,1428 & 0,0982 & -0,125 \\ \end{bmatrix} \hspace{2em} \style{font-size: 5px; color: #4CA6FF; }{(matriz \ inversa \ de \ A)}$

19 de 20