Uma inequação do 1° grau é a expressão que pode ser escrita numa das seguintes formas:

$ax + b > 0$;

$ax + b < 0$;

$ax + b \geq 0$;

$ax + b \leq 0$.

com $a$ ∈ $\mathbb{R}^{*}$ e $b \in \mathbb{R}$.

Vamos igualar a expressão $ax + b$ a zero para calcularmos a raiz.

$ax + b = 0$

$x = \dfrac{-b}{a}$ (Valor da raiz onde a reta corta o eixo $x$)

Vamos analisar os gráficos para os casos em que a função é crescente (a>0) e decrescente (a<0)

Para a > 0 (crescente) Conforme gráfico abaixo a inequacao será positiva para os valores de $x$ a direita da raiz e negativa para os valores de $x$ a esquerda da raiz.

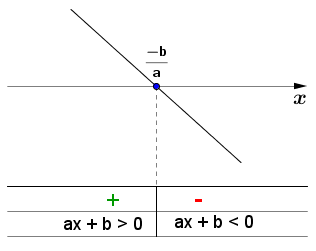
Para a < 0 (decrescente) Conforme gráfico abaixo a inequacao será negativa para os valores de $x$ a direita da raiz e positiva para os valores de $x$ a esquerda da raiz.