/ Matérias / Matemática /

Geometria Analítica: Estudo do Triângulo

Área do Triângulo $(S)$: Exemplos e Exercícios

Exemplo 2 - Um triângulo tem vértices P(2, 1), Q(2, 5) e R(x, 3), com x > 0. Sabendo-se que a área do triângulo é 20, a abscissa x do ponto R é:

A fórmula para o cálculo da área é:

$S = \dfrac{1}{2}.|d|$

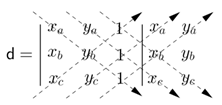
Substituindo as coordenadas dos vértices do triângulo temos:

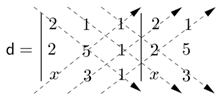
Portanto:

$d = 2.5.1+1.1.x+1.2.3-x.5.1-3.1.2-1.2.1$

$d = 10+x+6-5x-6-2$

$d = - 4x + 8$

aplicando a fórmula da área temos:

$S = \dfrac{1}{2} . |d|$

$20 = \dfrac{1}{2}.|-4x+8|$

$40 = |-4x+8|$

Caso que -4x+8 é maior que zero:

$-4x+8=40$

$-4x=32$

$x = \dfrac{32}{-4}$

$\colorbox{lightgreen}{$x = -8$}$

Caso que -4x+8 é menor que zero:

$-(-4x+8)=40$

$4x-8=40$

$x=\dfrac{48}{4}$

$ \colorbox{lightgreen}{$x=12$}$

mas x>0, logo x=12

x=12

3 de 6