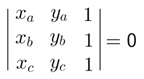/ Matérias / Matemática /

Geometria Analítica: Estudo do Triângulo

Área do Triângulo $(S)$

Seja o triângulo ABC de vértices $A(x_{a}, y_{a})$, $B(x_{b}, y_{b})$ e $C(x_{c}, y_{c})$ abaixo:

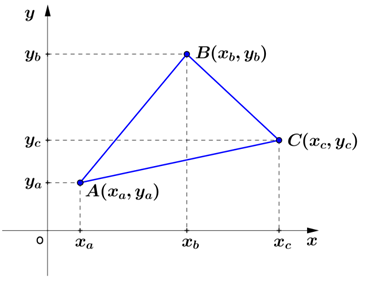
Fórmula:

$S = \dfrac{1}{2}.|d|$

onde:

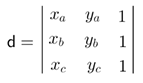
|d| - módulo do determinante das coordenadas do triângulo ABC.

Calculando o determinante pela regra de Sarrus temos:

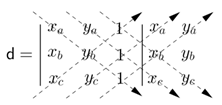
$d = x_{a}.y_{b}+y_{a}.x_{c}+x_{b}.y_{c}-x_{c}.y_{b}-y_{c}.x_{a}-x_{b}.y_{a}$

portanto:

$S = \dfrac{1}{2} . \left| x_{a}.y_{b}++y_{a}.x_{c}+x_{b}.y_{c}-x_{c}.y_{b}-y_{c}.x_{a}-x_{b}.y_{a} \right|$

Condição de existência de triângulo para três pontos:

Três pontos distintos do plano cartesiano $A(x_{a}, y_{a})$, $B(x_{b}, y_{b})$ e $C(x_{c}, y_{c})$ formarão um triângulo se eles não estiverem alinhados (pertencentes à mesma reta). Se eles estiverem alinhados, não existirá o triângulo ABC, portanto a área será nula.

$S = \dfrac{1}{2}.|d| = 0$

Portanto, d=0:

1 de 6

Área do Triângulo $(S)$

Área do Triângulo $(S)$: Exemplos e Exercícios

Baricentro do Triângulo

Baricentro do Triângulo: Exemplos e Exercícios