/ Matérias / Matemática /

Geometria Analítica: Estudo do Ponto

Distância entre dois pontos: Demonstração

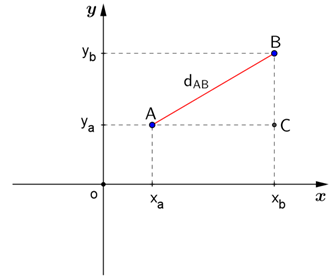
Para calcularmos a distância entre os pontos $A(x_{a}, y_{a})$ e $B(x_{b}, y_{b})$ aplicaremos o teorema de Pitágoras no triângulo retângulo ABC.

$(\overline{AB})^{2}=(\overline{AC})^{2}+(\overline{CB})^{2}$

Sabemos que:

Hipotenusa $\overline{AB} = d_{AB}$

Cateto $\overline{AC} = x_{b} - x_{a}$

Cateto $\overline{CB} = y_{b}- y_{a}$

Logo:

$(d_{AB})^{2} = (x_{b}-x_{a})^2 + (y_{b}-y_{a})^{2}$

$d_{AB} = \sqrt[]{(x_{b}-x_{a})^2 + (y_{b}-y_{a})^2 }$

6 de 11