/ Matérias / Matemática /

Geometria Analítica: Estudo da Reta

Equação segmentária da reta: Demonstração

Vamos analisar a figura abaixo:

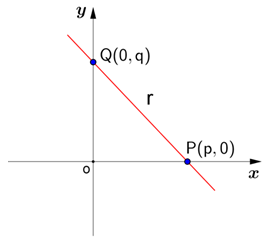
Aplicando a fórmula da condição de alinhamento de dois pontos e um ponto genérico da reta r temos:

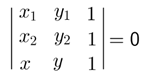
Substituindo as coordenadas dos pontos P(p, 0), Q(0, q) e um ponto genérico A(x, y) da reta r e calculando o determinante pela regra de Sarrus temos:

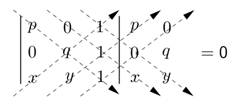
$pq + 0 + 0 - xq - yp - 0 = 0 $

$- xq - yp = - pq$

Multiplicando por (-1):

$xq + yp = pq$

Dividindo os termos por pq obtemos:

$\dfrac{xq}{pq}+\dfrac{yq}{pq}=\dfrac{pq}{pq}$

Simplificando os termos:

$\dfrac{x}{p}+\dfrac{y}{q}=1 \quad$ (conforme queríamos demonstrar)

15 de 25

Equação geral da reta

Equação geral da reta: Demonstração

Equação geral da reta: Exemplos e Exercícios

Equação reduzida da reta

Demonstração da equação reduzida, coeficiente angular e linear:

Demonstração da equação reduzida, coeficiente angular e linear: Exemplos e Exercícios

Equação da reta a partir de dois pontos da reta

Equação da reta a partir de dois pontos da reta: Demonstração

Equação da reta a partir de dois pontos da reta: Exemplos e Exercícios

Equação da reta a partir do coeficiente angular(m) e de um ponto

Equação da reta a partir do coeficiente angular(m) e de um ponto: Demonstração

Equação da reta a partir do coeficiente angular(m) e de um ponto $A(x_1, y_1)$ de $r$: Exemplos/Exercícios

Equação segmentária da reta

Equação segmentária da reta: Demonstração

Equação segmentária da reta: Exemplos e Exercícios

Retas horizontais e verticais

Retas paralelas

Retas coincidentes

Retas concorrentes

Ângulo entre duas retas

Ângulo entre duas retas: Demonstração do 1º Caso

Ângulo entre duas retas: Demonstração do 2º Caso

Distância de um ponto a uma reta

Distância de um ponto a uma reta: Exemplos e Exercícios