/ Matérias / Matemática /

Geometria Analítica: Estudo da Reta

Ângulo entre duas retas: Demonstração do 1º Caso

Nenhuma das retas é paralela ao eixo y.

Neste caso temos as duas situações abaixo para analisar:

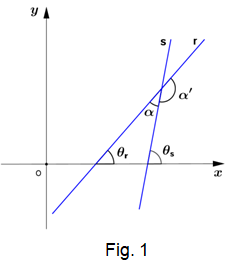
- Na figura 1 o teorema do ângulo externo diz que $\alpha = \theta_s - \theta_r$.

Portanto:

$tg \ \alpha = tg (\theta_s - \theta_r) = \dfrac{tg \ \theta_s - tg \ \theta_r}{1+ tg \ \theta_s . tg \ \theta_r}$

$tg \ \theta_s = m_s$

$tg \ \theta_r = m_r$

Então:

$tg \ \alpha = \dfrac{m_s - m_r}{1+ m_s . m_r}$

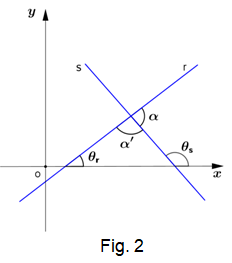
- Na figura 2 o teorema do ângulo externo diz que $\alpha ' = \theta_s - \theta_r$

Mas,

$\theta \ ' = 180º - \alpha$

Portanto:

$180º - \alpha = \theta_s - \theta_r$

$tg(180º - \alpha) = tg(\theta_s - \theta_r)$

$\dfrac{tg 180º - tg \ \alpha}{1+tg 180º . tg \ \alpha} = \dfrac{tg \ \theta_s - tg \ \theta_r}{1+ tg \ \theta_s . tg \ \theta_r}$

$\dfrac{0-tg \ \alpha}{1 + 0.tg \ \alpha} = \dfrac{tg \ \theta_s - tg \ \theta_r}{1 + tg \ \theta_s . tg \ \theta_r}$

$-tg \ \alpha = \dfrac{m_s - m_r}{1+m_s . m_r}$

Ou seja,

$tg \ \alpha = - \dfrac{m_s - m_r}{1+m_s . m_r}$

Sabemos que a tangente de um ângulo agudo é positivo, portanto as duas fórmulas acima podem ser resumidas em uma só conforme abaixo:

$\colorbox{lightgreen}{$tg \ \alpha = \left| \dfrac{m_s - m_r}{1+m_s . m_r} \right|$}$

Exemplo:

Determine o ângulo agudo entre as retas r: 2x + 3y + 2 = 0 e s: 3x - 2y +3 = 0.

Vamos determinar o coeficiente angular das retas reescrevendo-as na forma reduzida y = mx + q:

Reta r:

$-6x + 3y + 9 = 0$

$3y = 6x - 9 \quad$ (dividindo por 3)

$y = 2x - 3$

Comparando com a forma reduzida da equação concluímos que:

$\colorbox{yellow}{$m_r=2$}$

Reta s:

$6x + 2y - 4 = 0$

$2y = - 6x +4 \quad$ (dividindo por 2)

$y = -3x + 4$

Comparando com a forma reduzida da equação concluímos que:

$\colorbox{yellow}{$m_s=-3$}$

Aplicando a fórmula:

$tg \ \alpha = \left| \dfrac{m_s - m_r}{1+m_s . m_r} \right|$

$ tg \ \alpha = \left| \dfrac{-3-2}{1+(-3).(2)} \right|$

$ tg \ \alpha = \left| \dfrac{-3-2}{1-6} \right|$

$tg \ \alpha = \left| \dfrac{-5}{-5} \right|$

$tg \ \alpha = 1$

$\alpha = arctg \ 1$

$\alpha = 45º$

$\alpha = 45º$