/ Matérias / Matemática /

Geometria Analítica: Estudo da Circunferencia

Equação reduzida da circunferência: Demonstração

Para calcularmos a distância entre dois pontos $A(x_{a}, y_{a})$ e $B(x_{b}, y_{b})$ utilizamos a seguinte fórmula:

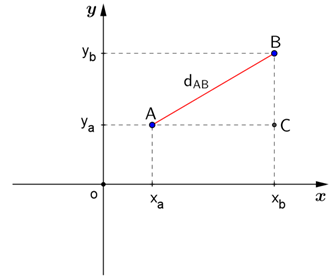
$d_{AB}=\sqrt[]{(x_{b}-x_{a})^{2}+(y_{b}-y_{a})^{2}}$

Portanto para calcularmos a distância $(d_{CP})$ entre o centro C(a,b) e um ponto P(x,y), da circunferência, utilizamos a seguinte fórmula:

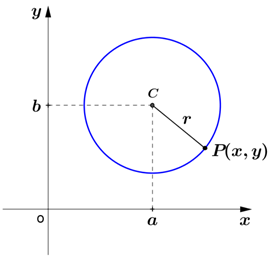
$d_{CP}=\sqrt[]{(x-a)^{2}+(y-b)^{2}}$

Sabemos que:

$d_{CP}=r$

portanto:

$r=\sqrt[]{(x-a)^{2}+(y-b)^{2}}$

Elevando os dois membros ao quadrado temos:

$(x-a)^{2}+(y-b)^{2}=r^{2}$

Veja que seja qual for o valor para x e y que você escolher, se eles respeitarem a equação acima então eles farão parte da circunferência, e que não existe nenhum ponto da circunferência que não respeita esta equação, ou seja, a equação acima descreve toda a circunferência.

Caso particular:

Quando o centro da circunferência está localizado na origem temos a=0 e b=0, portanto:

$(x-a)^{2}+(y-b)^{2}=r^{2}$

$(x-0)^{2}+(y-0)^{2}=r^{2}$

$\colorbox{lightgreen}{$x^{2}+y^{2}=r^{2}$}$

Chamamos a equação acima de equação reduzida da circunferência com o centro na origem.

2 de 9

Equação reduzida da circunferência

Equação reduzida da circunferência: Demonstração

Equação reduzida da circunferência: Exemplos e Exercícios

Equação geral da circunferência

Equação geral da circunferência: Exemplos e Exercícios

Posições relativas entre ponto e circunferência

Posições relativas entre ponto e circunferência: Exemplos e Exercícios

Posições relativas entre reta e circunferência

Posições relativas entre reta e circunferência: Exemplos e Exercícios