/ Matérias / Matemática /

Função do 2º Grau

Vértice de uma parábola

Sempre que uma função quadrática $(f(x) = ax^{2} + bx + c)$ corta o eixo das abcissas o eixo de simetria da parábola é uma reta perpendicular a este eixo no ponto médio entre as duas raízes passando pelo vértice da parábola $V\left(x_{v}, y_{v}\right)$.

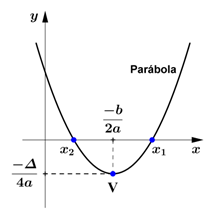
Portanto,

$x_{v} = \dfrac{-b}{2a}$

$y_{v} = \dfrac{-\Delta}{4a}$

Demonstração

Da fórmula de Bháskara sabemos que:

$x_{1} = \dfrac{-b+\sqrt{\Delta}}{2a}$

$x_{2} = \dfrac{-b-\sqrt{\Delta}}{2a}$

Cálculo da abcissa do vértice:

$x_v = \dfrac{x_1 + x_2}{2}$

$x_v = \dfrac{\dfrac{-b+\sqrt{\Delta}}{2a}+\dfrac{-b - \sqrt{\Delta}}{2a}}{2}$

$x_v = \dfrac{-b + \sqrt{\Delta} - b - \sqrt{\Delta}}{4a}$

$x_v = \dfrac{-2b}{4a}$

$x_v = \dfrac{-b}{2a}$

Cálculo da ordenada do vértice:

$y_v = f\left( x_v \right)$

$f\left( x_v \right) = ax_{v}^{2} + bx_{v} + c$

$y_v = f \left( \dfrac{-b}{2a} \right) = a. \left( \dfrac{-b}{2a} \right)^{2} + b.\left( \dfrac{-b}{2a} \right) + c$

$y_v = \dfrac{ab^2}{4a^2} - \dfrac{b^2}{2a} + c$

Simplificando temos:

$y_v = \dfrac{b^2}{4a} - \dfrac{b^2}{2a} + c$

$y_v = \dfrac{b^2 - 2b^2 + 4ac}{4a}$

$y_v = \dfrac{-b^2 + 4ac}{4a}$

$y_v = \dfrac{-\Delta}{4a}$

A Coordenada do vértice da parábola é $V \left( \dfrac{-b}{2a}, \dfrac{-\Delta}{4a} \right)$.

5 de 12

Definição de Função do Segundo grau

Raízes de uma função do segundo grau

Forma canônica de uma função do segundo grau

Gráfico da função do 2º grau (parábola)

Vértice de uma parábola

Estudo da função quadrática (parábola)

Estudo da função quadrática (parábola): 1º caso

Estudo da função quadrática (parábola): 2º caso

Estudo da função quadrática (parábola): 3º caso

Estudo da função quadrática (parábola): 4º caso

Estudo da função quadrática (parábola): 5º caso

Estudo da função quadrática (parábola): 6º caso