ent6 Função do 2º Grau: Gráfico da função do 2º grau (parábola) 
/ Matérias / Matemática /

Função do 2º Grau
4

Gráfico da função do 2º grau (parábola)

Chama-se parábola o lugar geométrico dos pontos de um plano que são equidistantes de uma reta r, denominada de diretriz, e de um ponto F localizado fora desta reta, que é o foco da parábola.
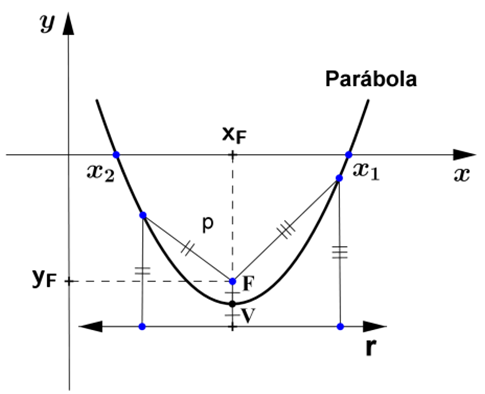
As coordenadas do foco $F\left(x_{F}, y_{F}\right)$ da parábola são:
$\left(\dfrac{-b}{2a} , - \dfrac{\Delta-1}{4a} \right)$

$\Delta = b^2 - 4ac$
A equação da diretriz r é:
$y + \dfrac{\Delta+1}{4a} = 0$
Determine o foco e a diretriz da parábola cuja função é $y = x^2 - x - 4$.
Dados:
a = 1
b = -1
c = -4
Vamos calcular o determinante da função:
$\Delta = b^{2} -4ac$

$\Delta = (-1)^{2}-4.1.(-4)$

$\Delta = 1 + 16$

$\Delta = 17$
Agora vamos calcular as coordenadas do foco F:
Cálculo da abscissa:
$x = \dfrac{-b}{2a}$

$x = \dfrac{-(-1)}{2.1}$

$x = \dfrac{1}{2}$
Cálculo da ordenada:
$y = - \dfrac{\Delta -1}{4a}$

$x = - \dfrac{17-1}{4.1}$

$x = - \dfrac{16}{4}$

$y=-4$
Cálculo da diretriz r:
$y + \dfrac{\Delta + 1}{4a}=0$

$y + \dfrac{17+1}{4.1} = 0$

$y + \dfrac{18}{4}=0$

$y+4,\hspace{-0.2em}5 = 0$

$y=4,\hspace{-0.2em}5$
A coordenada do foco é $F\left(\dfrac{1}{2},-4 \right)$ e a diretriz é $r:y=-4,\hspace{-0.2em}5$.




4 de 12







desenvolvido por


Copyright © 2023 Central Exatas
Todos os direitos reservados.