/ Matérias / Matemática /

Função do 2º Grau

Estudo da função quadrática (parábola): 4º caso

4º caso

$\Delta=0$ e $a<0$

Parábola com concavidade para baixo.

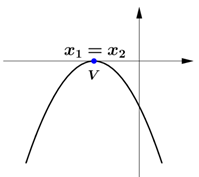
- Conjunto imagem da função quadrática

$Im(f) = \left\{ y \in \mathbb{R} \ | \ y \leq 0 \right\}$

- Vértice da parábola (ponto de máximo)

$V = \left( \dfrac{-b}{2a}, 0 \right)$

- Zeros da função quadrática

$x_1 = x_2 = \dfrac{-b}{2a}$

Exemplo: Esboce o gráfico da função $f(x) = -x² -2x -1$, indicando as coordenadas do vértice e os zeros da função quadrática.

Dados:
$a = -1$
$b = -2$
$c = -1$

Cálculo das coordenadas do vértice:

Cálculo da abscissa

$x=\dfrac{-b}{2a}$

$x=\dfrac{-(-2)}{2.(-1)}$

$x=\dfrac{2}{-2}$

$x=-1$

Cálculo da ordenada

$y = \dfrac{-\Delta}{4a}$

Cálculo do discriminante:

$\Delta = b^2-4ac$

$\Delta =(-2)^2 -4.(-1).(-1)$

$\Delta =4-4$

$\Delta =0$

Aplicando na fórmula temos:

$y=\dfrac{-0}{4.(-1)}$

$y = \dfrac{0}{-4}$

$y = 0$

Vértice

$V \left(-1 , 0 \right)$

Cálculo dos zeros da função:

$x = \dfrac{-b \pm \sqrt{\Delta}}{2a}$

$x = \dfrac{-(-2) \pm \sqrt{0}}{2.(-1)}$

$x=\dfrac{2 \pm 0}{-2}$

$x_1 = \dfrac{2 + 0}{-2} = \dfrac{2}{-2}$

$x_1=-1$

$x_2 = \dfrac{2-0}{-2} = \dfrac{2}{-2}$

$x_2 = -1$

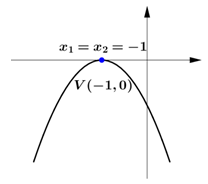
Gráfico da função $f(x) = -x² -2x - 1$:

10 de 12

Definição de Função do Segundo grau

Raízes de uma função do segundo grau

Forma canônica de uma função do segundo grau

Gráfico da função do 2º grau (parábola)

Vértice de uma parábola

Estudo da função quadrática (parábola)

Estudo da função quadrática (parábola): 1º caso

Estudo da função quadrática (parábola): 2º caso

Estudo da função quadrática (parábola): 3º caso

Estudo da função quadrática (parábola): 4º caso

Estudo da função quadrática (parábola): 5º caso

Estudo da função quadrática (parábola): 6º caso