Fechar 
-
-
- FÓRMULAS - GERAL
- FÓRMULAS DE CONJUNTOS
- FÓRMULAS DE ÁLGEBRA
- FÓRMULAS DE TRIGONOMETRIA
- FÓRMULAS DE EQUAÇÕES
- FÓRMULAS DE INEQUAÇÕES
- FÓRMULAS DE FUNÇÕES
- FÓRMULAS DE MATRIZES, DETERMINANTES E SISTEMAS LINEARES
- FÓRMULAS DE GEOMETRIA: 2D
- FÓRMULAS DE GEOMETRIA: 3D
- FÓRMULAS DE GEOMETRIA ANALÍTICA
- FÓRMULAS - OUTROS
-
-
xxxx
-
xxxx
Análise Combinatória
Princípio Multiplicativo: Exemplos e Exercícios
Exemplo 1 - Vamos analisar todos os resultados possíveis ao lançarmos uma moeda três vezes e observarmos a face de cima?
Podemos construir o que chamamos de diagrama de árvores para obtermos todos os resultados possíveis. Vamos adotar a letra K para cara e C para coroa.
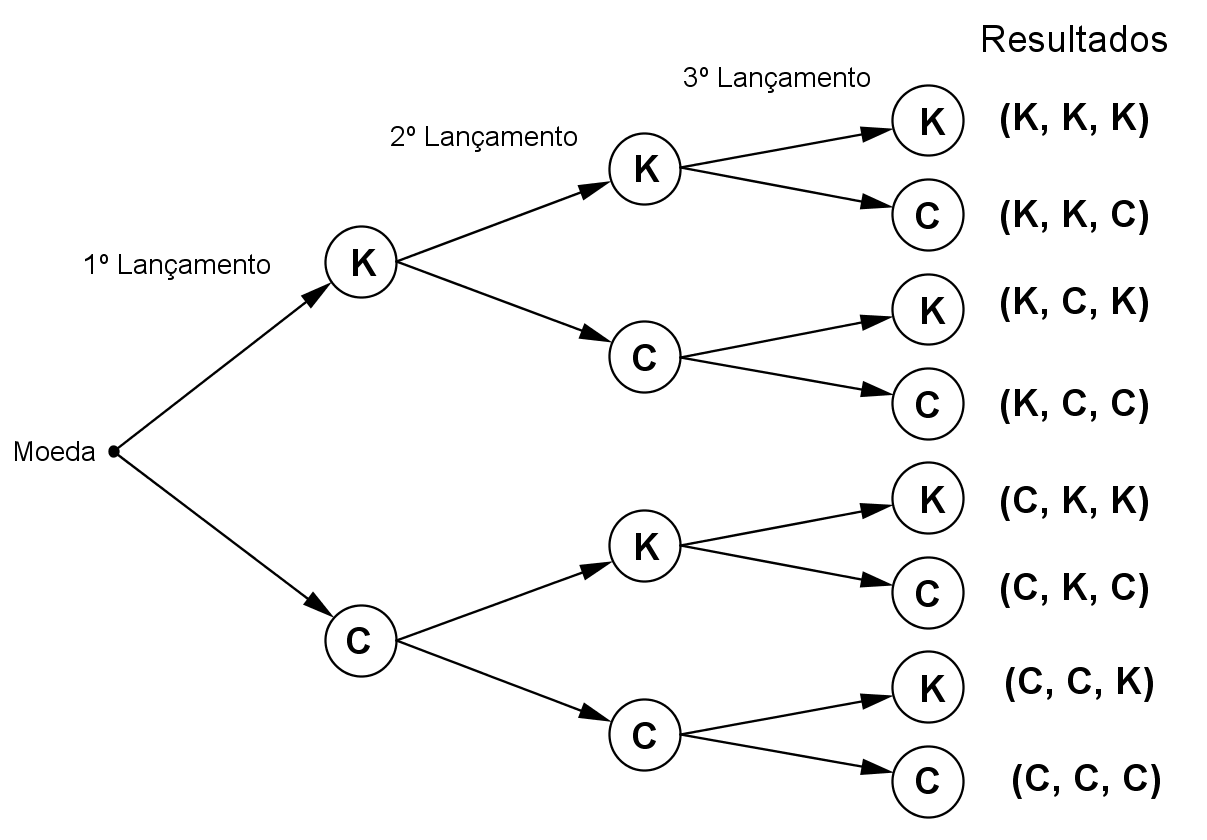
Pelo diagrama de árvores obtemos 8 resultados possíveis.
{(K, K, K), (K, K, C), (K, C, K), (K, C, C), (C, K, K), (C, K, C), (C, C, K), (C, C, C)}
{(K, K, K), (K, K, C), (K, C, K), (K, C, C), (C, K, K), (C, K, C), (C, C, K), (C, C, C)}
Agora vamos calcular utilizando o Princípio Multiplicativo.
Evento $E$: Lançar uma moeda três vezes.
Evento $E_{1}$ - 1º lançamento da moeda
$p_{1} = 2$ (duas possibilidades - K e C)
$p_{1} = 2$ (duas possibilidades - K e C)
Evento $E_{2}$ - 2º lançamento da moeda
$p_{2} = 2$ (duas possibilidades - K e C)
$p_{2} = 2$ (duas possibilidades - K e C)
Evento $E_{3}$ - 3º lançamento da moeda
$p_{3} = 2$ (duas possibilidades - K e C)
$p_{3} = 2$ (duas possibilidades - K e C)
Cálculo do número total de possibilidades do evento $E$:
$T_{p} = p_{1} . p_{2} . p_{3}$
$T_{p} = 2 . 2 . 2$
$T_{p} = 8 $
$T_{p} = 2 . 2 . 2$
$T_{p} = 8 $
8 possibilidades
3 de 54
1
Análise Combinatória: Definição
2
Princípio Multiplicativo: Definição (Princípio Fundamental da Contagem)
3
Princípio Multiplicativo: Exemplos e Exercícios
4
Princípio Multiplicativo: Exemplos e Exercícios
5
Princípio Multiplicativo: Exemplos e Exercícios
6
Princípio Multiplicativo: Exemplos e Exercícios
7
Princípio Multiplicativo: Princípio Multiplicativo e o conectivo "e"
8
Princípio Aditivo: Definição
9
Princípio Aditivo: Exemplos e Exercícios
10
Princípio Aditivo: Exemplos e Exercícios
11
Princípio Aditivo: Princípio Aditivo e o conectivo "ou"
12
Importância do Princípio Multiplicativo e do Princípio Aditivo
13
Fatorial: Definição
14
Fatorial: Por quê usar fatorial?
15
Arranjo Simples: Conceito
16
Arranjo Simples: Entendendo a Fórmula de Arranjo Simples
17
Arranjo Simples: Exemplos e Exercícios
18
Arranjo Simples: Exemplos e Exercícios
19
Arranjo Simples: Exemplos e Exercícios
20
Combinação Simples: Conceito
21
Combinação Simples: Entendendo a fórmula de Combinação Simples
22
Combinação Simples: Exemplos e Exercícios
23
Combinação Simples: Exemplos e Exercícios
24
Combinação Simples: Exemplos e Exercícios
25
Permutação Simples: Conceito
26
Permutação Simples: Entendendo a Fórmula de Permutação Simples
27
Permutação Simples: Exemplos e Exercícios
28
Permutação Simples: Exemplos e Exercícios
29
Permutação com Repetição: Conceito
30
Permutação com Repetição: Entendendo a Fórmula de Permutação com Repetição
31
Permutação com Repetição: Exemplos e Exercícios
32
Combinação com Repetição: Conceito
33
Combinação com Repetição: Entendendo a Fórmula de Combinação com Repetição
34
Combinação com Repetição: Exemplos e Exercícios
35
Combinação com Repetição: Exemplos e Exercícios
36
Combinação com Repetição: Exemplos e Exercícios
37
Permutação com Repetição: Exemplos e Exercícios
38
Permutação Circular: Conceito
39
Permutação Circular: Entendendo a Fórmula de Permutação Circular
40
Permutação Circular: Exemplos e Exercícios
41
Permutação Circular: Exemplos e Exercícios
42
Exemplos e Exercícios de Análise Combinatória com números
43
Exemplos e Exercícios de Análise Combinatória com números
44
Exemplos e Exercícios de Análise Combinatória com números
45
Exemplos e Exercícios de Análise Combinatória com números
46
Exemplos e Exercícios de Análise Combinatória com números
47
Exemplos e Exercícios de Análise Combinatória com números
48
Exemplos e Exercícios de Análise Combinatória com números
49
Exemplos e Exercícios de Análise Combinatória com números
50
Exemplos e Exercícios de Análise Combinatória que usam filas
51
Exemplos e Exercícios de Análise Combinatória que usam filas
52
Exemplos e Exercícios de Análise Combinatória que usam filas
53
Exemplos e Exercícios de Análise Combinatória que usam filas
54
Exemplos e Exercícios de Análise Combinatória que usam filas
