Análise Combinatória



Exemplos e Exercícios de Análise Combinatória com números
Exemplo 6 - Quantas senhas são possíveis formar com 3 algarismos distintos, sendo que o último algarismo é par?
Se os 1º ou 2º algarismo forem par ou ímpar, isto irá afetar o número de possibilidades para o 3º algarismo. Veja os exemplos abaixo:
1º algarismo = 5 (número ímpar)
2º algarismo = 7 (número ímpar)
3º algarismo $\rightarrow$ teremos 5 possibilidades (0,2,4,6 ou 8)
1º algarismo = 4 (número par)
2º algarismo = 7 (número ímpar)
3º algarismo $\rightarrow$ teremos 4 possibilidades (0,2,6 ou 8)
1º algarismo = 3 (número ímpar)
2º algarismo = 8 (número par)
3º algarismo $\rightarrow$ teremos 4 possibilidades (0,2,4 ou 6)
1º algarismo = 2 (número par)
2º algarismo = 4 (número par)
3º algarismo $\rightarrow$ teremos 3 possibilidades (0, 6 ou 8)
2º algarismo = 7 (número ímpar)
3º algarismo $\rightarrow$ teremos 5 possibilidades (0,2,4,6 ou 8)
1º algarismo = 4 (número par)
2º algarismo = 7 (número ímpar)
3º algarismo $\rightarrow$ teremos 4 possibilidades (0,2,6 ou 8)
1º algarismo = 3 (número ímpar)
2º algarismo = 8 (número par)
3º algarismo $\rightarrow$ teremos 4 possibilidades (0,2,4 ou 6)
1º algarismo = 2 (número par)
2º algarismo = 4 (número par)
3º algarismo $\rightarrow$ teremos 3 possibilidades (0, 6 ou 8)
Vamos separar o problema em duas partes para se o 1º algarismo é par ou ímpar, depois, iremos separar cada parte novamente em duas partes para se o 2º algarismo é par ou ímpar:
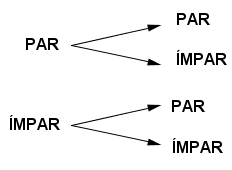
Caso que o 1º e 2º algarismos são pares:
Passo 1:
Para o 1º algarismo temos $5$ possibilidades (0,2,4,6,8):
$\underline{\hspace{0.6em} \hspace{0.2em} 5 \hspace{0.2em} \hspace{0.6em}} \hspace{0.7em}
\underline{\hspace{0.6em} \hspace{0.8em} \hspace{0.6em}} \hspace{0.7em}
\underline{\hspace{0.6em} \hspace{0.8em} \hspace{0.6em}}
$
Passo 2:
Para o 2º algarismo temos 5 possibilidades, menos o algarismo par que já foi escolhido no Passo 1, logo temos $4$ possibilidades:
$\underline{\hspace{0.6em} \hspace{0.2em} 5 \hspace{0.2em} \hspace{0.6em}} \hspace{0.7em}
\underline{\hspace{0.6em} \hspace{0.2em} 4 \hspace{0.2em} \hspace{0.6em}} \hspace{0.7em}
\underline{\hspace{0.6em} \hspace{0.8em} \hspace{0.6em}}
$
Passo 3:
Para o 3º algarismo temos 5 possibilidades, menos os dois algarismos pares escolhidos nos passos anteriores, logo temos $3$ possibilidades:
$\underline{\hspace{0.6em} \hspace{0.2em} 5 \hspace{0.2em} \hspace{0.6em}} \hspace{0.7em}
\underline{\hspace{0.6em} \hspace{0.2em} 4 \hspace{0.2em} \hspace{0.6em}} \hspace{0.7em}
\underline{\hspace{0.6em} \hspace{0.2em} 3 \hspace{0.2em} \hspace{0.6em}}
$
Pelo Princípio Multiplicativo temos $5.4.3 = 60$ possibilidades.
Fazendo os cálculos para cada um dos casos teremos:
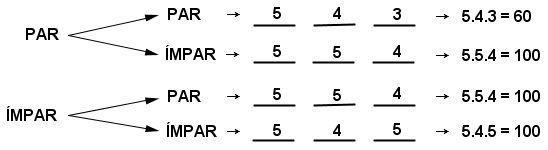
Pelo Princípio da Adição, temos: $60 + 100 + 100 + 100 = 360$ senhas.
360 senhas
1
Análise Combinatória: Definição
2
Princípio Multiplicativo: Definição (Princípio Fundamental da Contagem)
3
Princípio Multiplicativo: Exemplos e Exercícios
4
Princípio Multiplicativo: Exemplos e Exercícios
5
Princípio Multiplicativo: Exemplos e Exercícios
6
Princípio Multiplicativo: Exemplos e Exercícios
7
Princípio Multiplicativo: Princípio Multiplicativo e o conectivo "e"
8
Princípio Aditivo: Definição
9
Princípio Aditivo: Exemplos e Exercícios
10
Princípio Aditivo: Exemplos e Exercícios
11
Princípio Aditivo: Princípio Aditivo e o conectivo "ou"
12
Importância do Princípio Multiplicativo e do Princípio Aditivo
13
Fatorial: Definição
14
Fatorial: Por quê usar fatorial?
15
Arranjo Simples: Conceito
16
Arranjo Simples: Entendendo a Fórmula de Arranjo Simples
17
Arranjo Simples: Exemplos e Exercícios
18
Arranjo Simples: Exemplos e Exercícios
19
Arranjo Simples: Exemplos e Exercícios
20
Combinação Simples: Conceito
21
Combinação Simples: Entendendo a fórmula de Combinação Simples
22
Combinação Simples: Exemplos e Exercícios
23
Combinação Simples: Exemplos e Exercícios
24
Combinação Simples: Exemplos e Exercícios
25
Permutação Simples: Conceito
26
Permutação Simples: Entendendo a Fórmula de Permutação Simples
27
Permutação Simples: Exemplos e Exercícios
28
Permutação Simples: Exemplos e Exercícios
29
Permutação com Repetição: Conceito
30
Permutação com Repetição: Entendendo a Fórmula de Permutação com Repetição
31
Permutação com Repetição: Exemplos e Exercícios
32
Combinação com Repetição: Conceito
33
Combinação com Repetição: Entendendo a Fórmula de Combinação com Repetição
34
Combinação com Repetição: Exemplos e Exercícios
35
Combinação com Repetição: Exemplos e Exercícios
36
Combinação com Repetição: Exemplos e Exercícios
37
Permutação com Repetição: Exemplos e Exercícios
38
Permutação Circular: Conceito
39
Permutação Circular: Entendendo a Fórmula de Permutação Circular
40
Permutação Circular: Exemplos e Exercícios
41
Permutação Circular: Exemplos e Exercícios
42
Exemplos e Exercícios de Análise Combinatória com números
43
Exemplos e Exercícios de Análise Combinatória com números
44
Exemplos e Exercícios de Análise Combinatória com números
45
Exemplos e Exercícios de Análise Combinatória com números
46
Exemplos e Exercícios de Análise Combinatória com números
47
Exemplos e Exercícios de Análise Combinatória com números
48
Exemplos e Exercícios de Análise Combinatória com números
49
Exemplos e Exercícios de Análise Combinatória com números
50
Exemplos e Exercícios de Análise Combinatória que usam filas
51
Exemplos e Exercícios de Análise Combinatória que usam filas
52
Exemplos e Exercícios de Análise Combinatória que usam filas
53
Exemplos e Exercícios de Análise Combinatória que usam filas
54
Exemplos e Exercícios de Análise Combinatória que usam filas





